Exploiter la puissance du diagramme de Bode pour garantir la stabilité d'un circuit

Dans les années 1930, Hendrik Wade Bode a créé une approche gain/phase intuitive, avec la stabilité du circuit comme seul objectif. Cela a donné lieu à ce que l'on appelle maintenant le diagramme de Bode, un affichage graphique intuitif du gain, de la phase et du système de contre-réaction d'un circuit ou d'un amplificateur par rapport à la fréquence.

Compte tenu de son utilité et de son importance, prenons quelques instants pour appliquer une technique d'analyse de la stabilité de Bode pour étudier l'ordre de grandeur du facteur de contre-réaction d'un circuit et d'un amplificateur à boucle ouverte, en décibels (dB), et sa réponse en phase (en degrés). Cet article de blog étudie ces concepts et propose des solutions pour éviter de concevoir un circuit « bourdonnant » lorsque votre objectif principal est la stabilité de fréquence.

Pour mettre en pratique cette technique, vous pouvez télécharger une version imprimable d'un diagramme de Bode à partir des ressources dans le manuel en ligne DigiKey Innovation Handbook.

Diagramme de Bode unipolaire

La configuration du circuit unipolaire permet aux signaux V_IN CC de passer directement à V_OUT, tandis qu'à des fréquences d'entrée plus élevées, la valeur V_OUT est égale à zéro décibel (dB). La construction du diagramme de Bode est simple. Les unités de l'axe Y correspondent à la fréquence logarithmique, et l'axe X représente le gain en décibels ou la phase en degrés. Il existe de nombreuses formules que vous pouvez appliquer lors de la conception d'un diagramme de Bode, mais intéressons-nous à l'approche pour une solution rapide.

La simplicité du diagramme de Bode tient au fait que le tracé des graphiques ne nécessite qu'un outil pour tracer des lignes droites et la connaissance de quelques règles (Figure 1).

Figure 1 : Un diagramme de Bode unipolaire illustrant le décalage d'ordre de grandeur et de phase utilise des lignes droites pour représenter la réponse en fréquence et en phase du circuit. (Source de l'image : Bonnie Baker)

Les deux diagrammes de la Figure 1 représentent la fréquence par rapport au gain et à la phase pour une paire résistance/condensateur unipolaire. Les plages de fréquences de l'axe X du diagramme du haut et du bas varient de 1 hertz (Hz) à 10 mégahertz (MHz). La plage de l'axe Y du diagramme du haut varie de 0 dB à 100 dB, avec la valeur de signal de 1 Hz qui équivaut à 100 dB. Cette valeur correspond à un facteur de gain de 100 000 x V_IN. La courbe bleue représente la réponse de gain avec un circuit unipolaire à f_P ou 100 Hz, où R est égal à 159 kilohms (kΩ), et C est égal à 10 nanofarads (nF).

À mesure que la fréquence augmente et dépasse la fréquence du pôle (f_P), la courbe bleue diminue à un taux de -20 dB/décade ou -6 dB/octave. Ce taux d'atténuation est la première règle de base du diagramme de Bode : chaque pôle du circuit diminue à un taux de -20 dB/décade, à partir du niveau de la fréquence du pôle. Par conséquent, si deux pôles atténuent V_OUT dans la même plage de fréquences, le taux d'atténuation est de -40 dB/décade.

Le diagramme du bas à la Figure 1 représente la phase de ce circuit unipolaire. À 1 Hz, la phase du réseau R/C est de 0 degré (°). À une décade avant f_P, ou dans ce cas à 10 Hz, la phase unipolaire commence à diminuer à un taux de -45°/décade vers sa valeur cible de -90°.

Plusieurs règles s'appliquent à la réponse en phase du pôle. La deuxième règle de base du diagramme de Bode pour le circuit polaire est que la phase est égale à -45° à f_P. Les troisième et quatrième règles du diagramme de Bode décrivent le point de phase d'atténuation et d'achèvement. La phase unipolaire commence à diminuer une décade avant la fréquence du pôle (f_P) et finit par se stabiliser une décade après f_P à -90°.

Diagramme de Bode à zéro simple

Le diagramme de Bode à zéro simple reflète les règles opposées au diagramme de Bode unipolaire. Les positions varient avec les mêmes valeurs pour R et C afin d'empêcher les tensions V_IN CC, tout en autorisant la fréquence supérieure à traverser le condensateur (Figure 2).

Figure 2 : Diagramme de Bode à zéro simple illustrant le décalage d'ordre de grandeur et de phase. (Source de l'image : Bonnie Baker)

À mesure que la fréquence augmente au-delà de f_Z, la courbe bleue augmente à un taux de +20 dB/décade. Le diagramme du bas de la Figure 2 représente la phase de ce circuit à zéro simple. À une décade avant f_Z, la phase à zéro simple commence à augmenter à un taux de +45°/décade vers sa valeur cible de +90°. La phase du circuit zéro est égale à +45° à f_Z.

Pour résumer les valeurs de la Figure 1, l'emplacement du pôle est f_P, et l'ordre de grandeur du gain après f_P présente une pente de -20 dB/décade. La phase présente une pente de -45°/décade jusqu'à f_P, et commence son atténuation à 0,1 x f_P et se stabilise à -90° à 10 x f_P. Pour résumer les valeurs de la Figure 2, l'emplacement du zéro est f_Z, et l'ordre de grandeur du gain après f_Z présente une pente de +20 dB/décade. La phase présente une pente de +45°/décade jusqu'à f_Z, et commence son atténuation à 0,1 x f_Z et se stabilise à +90° à 10 x f_Z.

Diagramme de Bode d'amplificateur en boucle ouverte

Le fonctionnement de fréquence du produit d'amplificateur opérationnel standard peut présenter plusieurs pôles et plusieurs zéros dans la fonction de transfert, à partir d'une fréquence sub-hertz jusqu'à la fréquence de coupure de 0 dB. Il n'y a rien de magique dans le diagramme de Bode d'un amplificateur. Il suffit de suivre les règles (Figure 3).

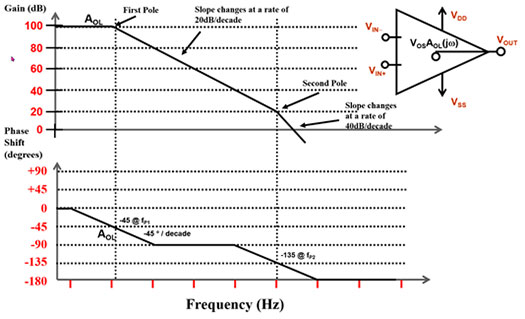Figure 3 : Diagramme de Bode possible pour un amplificateur opérationnel illustrant le décalage d'ordre de grandeur et de phase. (Source de l'image : Bonnie Baker)

La Figure 3 illustre un exemple d'amplificateur opérationnel avec deux pôles (f₁ et f₂) dans la fonction de transfert. Avec les deux pôles, le gain diminue à chaque fois de -20 dB/décade, et la phase diminue jusqu'à un total de -180 degrés.

À ce stade, nous avons un bon point de départ pour construire des diagrammes de Bode, mais observons maintenant le monde réel, où il y a également un système de contre-réaction.

Stabilité du système d'amplificateur en boucle fermée

Vous trouverez toujours un réseau de contre-réaction à proximité si vous prenez le temps d'observer des circuits d'amplificateur opérationnel. Le réseau de contre-réaction d'un amplificateur opérationnel classique contient un élément d'anticipation de gain (A_OL(jω)) et l'élément de contre-réaction (β(jω)).

Figure 4 : Réseau de contre-réaction d'un amplificateur opérationnel classique avec un élément d'anticipation (AOL(jω)) et un élément de contre-réaction (β(jω)). (Source de l'image : Bonnie Baker)

Dans la Figure 4, le gain en boucle ouverte de l'amplificateur opérationnel (A_OL) est relativement important, et le facteur de contre-réaction est relativement petit. Cette configuration renvoie la sortie vers la borne inverseuse, ce qui crée une condition de contre-réaction négative, où la contre-réaction permet de contrôler la sortie. Nous utiliserons l'inverse de β ou 1/β pour déterminer la stabilité d'un circuit d'amplificateur opérationnel.

Le moyen le plus facile de calculer 1/β est de placer une source, appelée V_STABILITY, au niveau de l'entrée non inverseuse de l'amplificateur opérationnel. Cette stratégie de calcul constitue une excellente solution pour déterminer la stabilité du circuit (Figure 5).

Figure 5 : Un circuit d'amplificateur opérationnel non inverseur (a) et un circuit d'amplificateur inverseur (b) présentent tous deux une source de tension V_STABILITY fictive au niveau de leur entrée non inverseuse pour permettre un calcul précis du facteur 1/β du circuit, ou gain de bruit. (Source de l'image : Bonnie Baker)

Si vous examinez les circuits de la Figure 5, vous remarquerez que les circuits de contre-réaction de la borne non inverseuse vers la sortie sont identiques. L'emplacement de la source de tension V_STABILITY permet un calcul précis du facteur 1/β du circuit, ou gain de bruit.

L'analyse de la stabilité 1/β utilise V_STABILITY. En supposant que le gain en boucle ouverte de l'amplificateur opérationnel est infini, la fonction de transfert des deux circuits est :

Équation 1

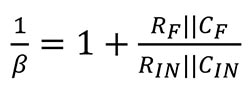Équation 2

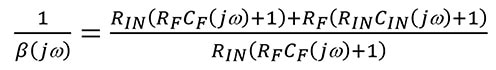Équation 3

Lorsque les composants de fréquence de l'Équation 3, jω, sont nuls :

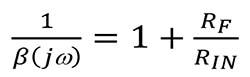Équation 4

À mesure que jω tend vers l'infini dans l'Équation 3 :

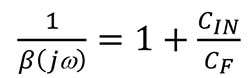Équation 5

Les fréquences pour le zéro (f_Z) et le pôle (f_P) de 1/β sont :

Équation 6

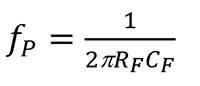Équation 7

Les diagrammes de Bode des courbes d'analyse de stabilité de 1/β conformes aux règles définies ci-dessus sont illustrés à la Figure 6.

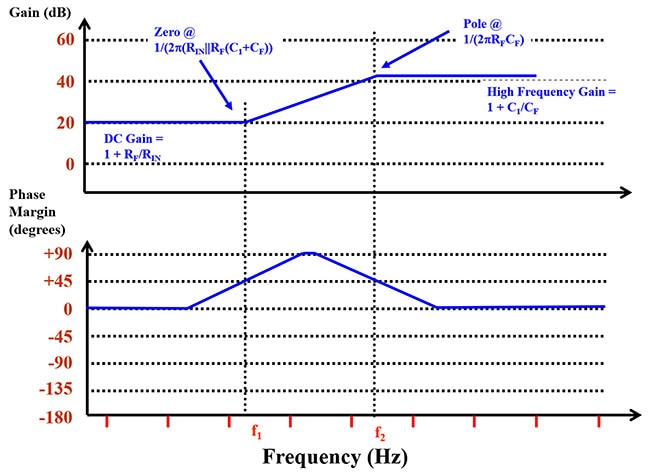Figure 6 : La réponse en fréquence 1/β est la même pour la Figure 5 a et b. Le zéro intervient à une fréquence inférieure, et le pôle intervient à une fréquence supérieure. (Source de l'image : Bonnie Baker)

La Figure 6 décrit la réponse en fréquence et en phase du facteur 1/β, ou gain de bruit, du circuit d'amplificateur opérationnel. Cette figure résume les équations 4 à 7 sous forme graphique. Les équations 4 et 5 définissent le gain CC et le gain ¥, de façon inclusive. Les équations 6 et 7 identifient le zéro et le pôle du circuit, de façon inclusive. Les informations dans les Figures 3 et 6 fournissent la première étape dans l'établissement de la stabilité d'un circuit d'amplificateur opérationnel en définissant la fonction de transfert du système et l'emplacement des pôles et des zéros. La dernière étape consiste à superposer les Figures 3 et 6 dans un seul et même diagramme.

Détermination de la stabilité du système

L'intersection ou le taux de fermeture du gain en boucle ouverte et du gain en boucle fermée définit le décalage de phase du circuit. Généralement, un taux de fermeture inférieur ou égal à 30 dB indique un circuit stable. Un taux de fermeture supérieur à 30 dB tend vers un circuit instable (Figure 7).

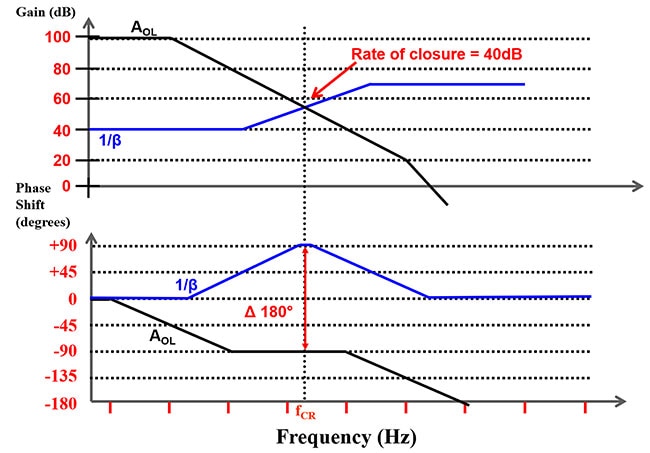Figure 7 : Superposition de la réponse en gain et en phase AOL avec la réponse en gain et en phase 1/β d'un amplificateur opérationnel. (Source de l'image : Bonnie Baker)

Dans la Figure 7, le taux de fermeture entre les courbes de gain A_OL et 1/β est égal à 40 dB. Un taux de fermeture de 40 dB indique un décalage de phase supérieur à 135°, ce qui montre un circuit instable. Avec cette configuration, le taux de fermeture de 180° produit un circuit qui oscille.

Il existe de nombreuses solutions au problème ci-dessus. Il est possible de faire varier les valeurs de résistance ou de condensateur en déplaçant les fréquences de pôle et de zéro. Une autre alternative consiste à sélectionner un autre amplificateur opérationnel (Figure 8).

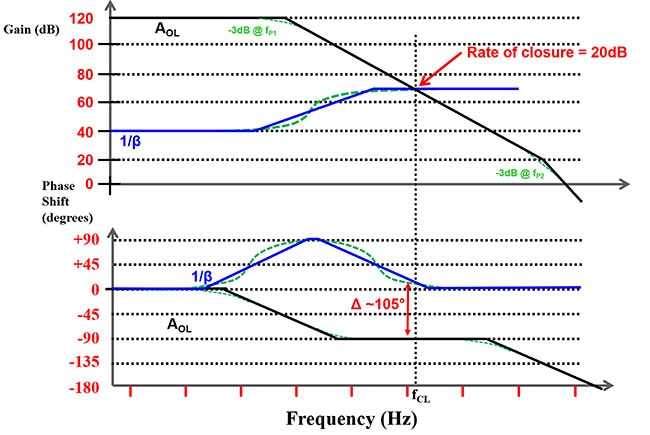Figure 8 : Utilisation d'un amplificateur opérationnel avec une bande passante supérieure à celle de l'amplificateur opérationnel de la Figure 7 sans changer les fréquences de zéro et de pôle. (Source de l'image : Bonnie Baker)

Dans la Figure 8, la bande passante de l'amplificateur opérationnel est approximativement deux décades supérieure, sans changement du réseau 1/β. Les lignes en pointillés verts reflètent les calculs réels et fournissent un diagramme de Bode plus réaliste. L'augmentation de la bande passante de l'amplificateur change le taux de fermeture de 40 dB à 20 dB. Le décalage de phase qui en résulte est maintenant de ~105°, ce qui indique un circuit stable.

Les lignes en pointillés verts de la Figure 8 vont au-delà de la création du diagramme de Bode à l'aide d'une règle et d'un crayon en incluant la réponse dans le monde réel.

Mesure du gain et de la phase du circuit

La mesure du gain et de la phase d'un circuit d'amplificateur nécessite un générateur de fonctions qui fournit le signal d'entrée, ainsi qu'un analyseur de réseau (Figure 9). L'illustration représente le générateur de fonctions à balayage analogique RF 3 GHz LS3081B de Tabor Electronics.

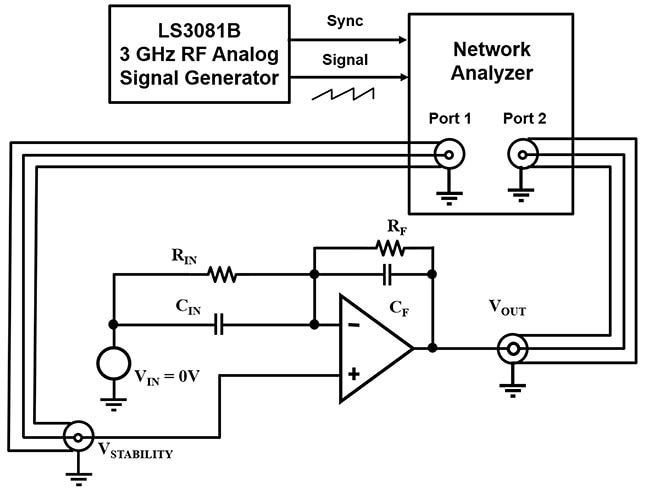Figure 9 : Configuration de la mesure de gain et de phase pour le circuit d'amplificateur inverseur de la Figure 5 b. (Source de l'image : Bonnie Baker)

Dans la Figure 9, l'application du signal d'entrée du générateur de fonctions intervient au niveau du nœud du port 1 vers V_STABILITY. Le signal se propage à travers le circuit d'amplificateur vers la sortie du circuit (V_OUT), où l'analyseur de réseau capture le signal au niveau du port 2 et le compare au signal du port 1 du générateur de fonctions.

Conclusion

Pour concevoir des circuits d'amplificateur opérationnel stables, le diagramme de Bode est un outil extrêmement utile à avoir. Les pouvoirs du diagramme de Bode deviennent évidents en observant des circuits à plusieurs pôles ou à plusieurs zéros, où le taux de fermeture entre le gain en boucle ouverte de l'amplificateur et le réseau de contre-réaction définit rapidement la stabilité du circuit.

Même si cet article de blog peut vous aider à maîtriser l'utilisation du diagramme de Bode en montrant l'utilisation simple d'une règle sur du papier millimétré pour estimer le gain par rapport à la phase d'un circuit à pôle et zéro de premier ordre, la meilleure façon d'apprendre est la pratique. Encore une fois, vous pouvez commencer par télécharger une version imprimable d'un diagramme de Bode à partir des ressources dans le manuel en ligne DigiKey Innovation Handbook.