Principes de base analogiques - 4e partie : optimisation des CAN delta-sigma pour un faible bruit

Note de l'éditeur : Les convertisseurs analogique-numérique (CAN) connectent le monde analogique au monde numérique et sont donc un élément fondamental de tout système électronique qui se connecte au monde réel. Ils sont également un facteur déterminant quant aux performances d'un système. Cette série explore les principes fondamentaux des CAN, leurs différents types et leur application. La 1ère partie de cette série sur les principes de base analogiques est consacrée aux CAN SAR. La 2e partie traite des convertisseurs delta-sigma. La 3e partie explore les CAN pipelines. Ici, la 4e partie montre comment les CAN delta-sigma peuvent générer des résultats de bruit ultrafaible. La 5e partie explore les problèmes de commande d'entrée complexes pour les CAN SAR.

La topologie de circuit intégré delta-sigma (ΔƩ) continue d'apparaître dans les convertisseurs analogique-numérique (CAN), offrant des solutions haute résolution, haute intégration et basse consommation pour les applications de contrôle de processus, de mesure de température de précision et de pesage.

Ce qui est curieux avec ce type de convertisseur, c'est qu'il commence par une conversion de 1 bit avec un rapport signal/bruit (SNR) théorique de 7,78 décibels (dB), ce qui équivaut à un bruit de 2 volts (V_RMS) dans un système de 5 V. À partir de là, le CAN peut se transformer en un véritable convertisseur delta-sigma 24 bits fournissant un SNR théorique de 146 dB, ce qui équivaut à un bruit efficace de 244 nanovolts (nV) dans un système de 5 V.

Ce saut de résolution de 1 à 24 bits s'appuie sur des algorithmes de suréchantillonnage, des modulateurs de mise en forme du bruit et des filtres numériques pour réduire le bruit de quantification et augmenter le rapport signal/bruit. Il existe un moyen d'éviter la complexité du convertisseur ΔƩ et le bruit associé en utilisant à la place un étage d'entrée d'amplificateur alimentant un CAN à registre d'approximations successives (SAR) de 12 ou 16 bits. Cette approche de conception fonctionne, mais elle nécessite davantage de circuits intégrés sur la carte à circuit imprimé et une nomenclature accrue.

Il existe une meilleure façon de s'attaquer au problème du bruit : l'aborder de front avec un CAN ΔƩ à bruit ultrafaible.

Cet article traite brièvement de l'application cible à faible bruit et de la manière dont le CAN ΔƩ est conçu en interne pour répondre à cette exigence. Il présente ensuite deux CAN ΔƩ de Texas Instruments — l'un mettant l'accent sur la précision 24 bits, l'autre sur la précision 32 bits — tout en montrant comment tirer parti du filtrage numérique robuste dans les deux cas.

Où se situe le CAN ΔƩ

D'un point de vue analogique, les ingénieurs ont besoin de divers degrés de précision pour mesurer la sortie des capteurs optiques, de température, de pression et de cellules de charge. Fondamentalement, les amplificateurs améliorent la capacité des concepteurs à quantifier ces petites occurrences, dans la plupart des cas proches de CC, analogiques. La numérisation progressive a entraîné un changement de perspective et de capacités, tout en améliorant la capacité à stocker et à modifier les signaux des capteurs.

Le chemin de signal de capteur typique vers la capture numérique commence par le capteur, passe par les étages de gain, de multiplexage et de filtrage, puis par le CAN (Figure 1a).

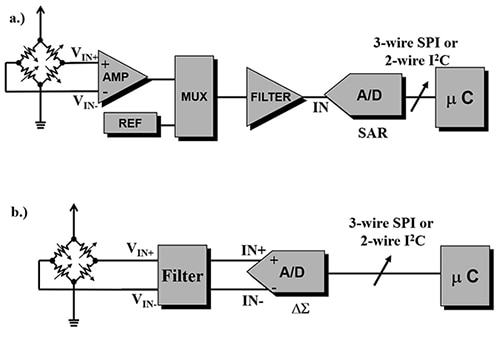Figure 1 : Deux techniques de numérisation d'un signal de capteur utilisent les CAN SAR (a) ou les CAN ΔƩ (b). Pour les circuits haute résolution, le CAN SAR nécessite une amplification et un filtre actif de cinquième ordre, tandis que le CAN ΔƩ requiert un filtre passif analogique de premier ordre en frontal. (Source de l'image : A Baker's Dozen: Real Analog Solutions for Digital Designers, B. Baker, ISBN 0-7506-7819-4)

Le convertisseur de la Figure 1a est un CAN SAR qui peut effectuer des conversions de 12 à 18 bits et fonctionner à des taux de conversion atteignant 10 méga-échantillons par seconde (Méch./s). Le convertisseur 16 bits fournit 2¹⁶ ou 65 536 segments. Dans un système 5 V, le bit le moins significatif (LSB) est 5 V/2¹⁶²⁹⁸ ou 76,3 microvolts (mV), avec un SNR théorique égal à 98 dB. Il est possible d'obtenir une granularité plus élevée en exerçant un gain analogique avant le convertisseur SAR.

La chaîne de signaux ΔƩ (Figure 1b) améliore la résolution de la chaîne de signaux avec un seul convertisseur, ce qui réduit également la nomenclature. Le CAN ΔƩ peut fournir des conversions de 16 à 32 bits. Dans cette chaîne de signaux, le CAN ΔƩ 24 bits fournit 2²⁴ ou 16 777 216 segments. Dans un système 5 V, le bit le moins significatif est donc de 5 V/2²⁴, ou 298 nV, avec un SNR théorique égal à 146 dB. Ce niveau de résolution rapproche la granularité du convertisseur des capacités du capteur.

Le CAN ΔƩ 24 bits est plus lent en raison des filtres numériques internes qui nécessitent du temps pour mettre en œuvre les calculs de filtrage. Les débits de données de sortie typiques de ce convertisseur s'étendent de quelques hertz à 1 Méch./s. Notez que le filtre analogique est maintenant un filtre résistance-capacité (RC) du premier ordre économique au lieu d'un filtre analogique du cinquième ordre complexe à trois amplificateurs opérationnels.

Les différences de bruit entre ces deux approches sont claires : le CAN ΔƩ avec son faible bruit surpasse le CAN SAR (Tableau 1).

*Note : SNR = 6,02 N + 1,76, où N est le nombre de bits

Tableau 1 : Segments CAN, LSB et SNR théorique avec tension d'entrée pleine échelle de 5 V pour un CAN SAR 16 bits et un CAN ΔƩ 24 bits. (Source des données : DigiKey Electronics)

Le CAN ΔƩ offre une excellente solution pour les solutions de capteurs, comme la température, la pression et la cellule de charge, où la spécification de la vitesse n'est pas critique ; cependant, la précision est primordiale. Ce CAN peut convertir ces petites valeurs de tension en utilisant des techniques numériques, au lieu de techniques de réduction du bruit analogiques.

Dans le CAN ΔƩ

L'intérieur du CAN ΔƩ est à 80 % numérique. Généralement, le convertisseur reçoit le signal d'entrée et transforme immédiatement ce signal analogique en signal numérique. Le convertisseur combine ensuite ce signal numérique avec les conversions ultérieures du modulateur dans un étage de filtre numérique où le signal 1 bit accumulé est converti en plusieurs bits. Le convertisseur envoie ensuite en série la conversion multibit finale au microcontrôleur en attente via l'étage de sortie numérique.

Le signal analogique passe d'abord à travers un filtre antirepliement (AAF) du premier ordre externe. Ensuite, le modulateur de mise en forme du bruit (NS) prend le signal analogique et génère un flux de 1 bit à la fréquence d'horloge du convertisseur dans le filtre numérique (Figure 2).

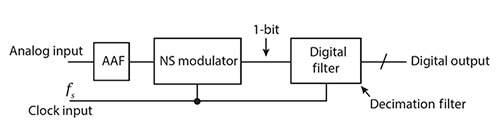Figure 2 : Le ΔƩ typique fait passer le signal analogique dans un filtre antirepliement du premier ordre, génère un flux de 1 bit à l'aide du modulateur NS, puis produit un résultat multibit à la sortie numérique vers un microcontrôleur. (Source de l'image : CMOS: Mixed-Signal Circuit Design, 2^nd Edition, J. Baker, ISBN 978-0-470-29026-2)

Le filtre numérique enregistre plusieurs codes du flux de 1 bit et crée un résultat multibit complet dans le filtre numérique. Ces résultats multibits sont transmis en série via la sortie numérique.

Le modulateur ΔƩ

Le nombre de boucles de rétroaction/d'intégrateurs détermine l'ordre du modulateur ΔƩ. Le modulateur CAN ΔƩ du premier ordre a un seul intégrateur et une seule boucle de rétroaction (Figure 3).

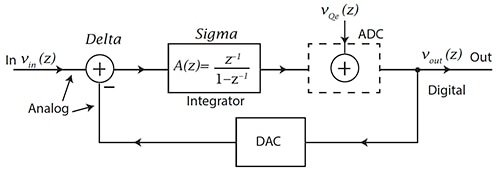Figure 3 : Modulateur du premier ordre avec un intégrateur analogique et un CAN 1 bit et un CNA dans la boucle de rétroaction. V_Qe(z) est le bruit CAN de quantification. (Source de l'image : CMOS: Mixed-Signal Circuit Design, 2^nd Edition, J. Baker, ISBN 978-0-470-29026-2)

Dans la Figure 3, le signal analogique (V_IN(z)) entre dans la partie Delta (Δ) du modulateur. Le signal analogique passe ensuite par un étage d'intégrateur ou un étage Sigma (Ʃ) jusqu'à un CAN de 1 bit (avec une fréquence d'échantillonnage de f_S, comme illustré à la Figure 2), qui peut être un comparateur. Ce signal numérisé, désormais cadencé, est renvoyé au convertisseur numérique-analogique (CNA) 1 bit et passe également à V_OUT(z) dans l'étage Δ. Le CNA 1 bit présente une tension analogique à soustraire du signal d'entrée analogique, V_IN(z). La fonction de transfert pour ce modulateur du premier ordre est la suivante :

Équation 1

En raison de l'intégrateur et de la boucle de rétroaction, le modulateur met en œuvre un algorithme de mise en forme du bruit sur le flux de données de sortie numérique du modulateur (Figure 4).

Figure 4 : Fonction de mise en forme du bruit à la sortie du modulateur ΔƩ, où la fonction de transfert du bruit (NTF) est égale à 1-z^-1, où la fréquence normalisée 0,5 est égale à F_S/2. (Source de l'image : Understanding Delta-Sigma Data Converters, Schreier, Temes, ISBN 0-471-46585-2)

Dans la Figure 4, la caractéristique de mise en forme du bruit est la première étape vers la réduction du bruit de quantification à 1 bit de conversion. Le bruit étant poussé avec succès dans les hautes fréquences, un filtre numérique passe-bas complète le processus de réduction du bruit.

Les modulateurs d'ordres supérieurs contiennent des intégrateurs et des boucles de rétroaction supplémentaires. Par exemple, un modulateur du troisième ordre a trois intégrateurs et trois boucles de rétroaction. La fonction de mise en forme du bruit change avec l'ordre du modulateur en réduisant le bruit près de CC et en augmentant le bruit mis en forme.

Les modulateurs d'ordres supérieurs offrent des performances améliorées au détriment d'un matériel en silicium plus important, et d'une stabilité et d'une portée des signaux réduites.

Les filtres numériques ΔƩ

Le CAN ΔƩ fonctionne en utilisant le suréchantillonnage (OS). Le suréchantillonnage est le rapport entre la fréquence d'échantillonnage du modulateur (F_S) et le débit de données de sortie du CAN (F_D), selon l'Équation 2 :

Équation 2

Le suréchantillonnage améliore le bruit du CAN ΔƩ en limitant numériquement la largeur de bande des données à bruit mis en forme avec un ou plusieurs filtres numériques passe-bas.

Les deux filtres numériques fréquemment utilisés dans les CAN ΔƩ sont les filtres sin(pf)/pf (sinc) et les filtres à réponse impulsionnelle finie (RIF) à phase linéaire. L'implémentation de filtre numérique des CAN ΔƩ 24 bits ADS1235 et des CAN ΔƩ 32 bits ADS1262 et ADS1263 de Texas Instruments (l'ADS1263 intègre un CAN ΔƩ 24 bits auxiliaire destiné aux mesures d'arrière-plan), offre le choix entre l'utilisation des filtres sinc exclusivement, ou une combinaison des filtres sinc suivis par les filtres RIF (Figure 5).

Figure 5 : Le CAN ΔƩ 24 bits ADS1235 permet l'utilisation de filtres sinc exclusivement, ou une combinaison de filtres sinc suivis de filtres RIF. (Source de l'image : Texas Instruments)

Dans la Figure 5, le filtre sinc est un filtre numérique passe-bas. La sortie (w(n)) d'un filtre sinc est calculée à l'aide de l'Équation 3 :

Équation 3

La fonction de transfert du domaine z est :

Équation 4

La réponse en fréquence est :

Équation 5

Dans la Figure 5, Sinc^N équivaut à N filtres sinc identiques en série. La réponse graphique amplitude/fréquence du filtre sinc a l'apparence d'un peigne (Figure 6).

Figure 6 : Dans l'ADS1262/63, à 2400 échantillons par seconde (éch./s), les nombreux filtres numériques sinc — où sinc2 est équivalent à deux filtres sinc identiques en série et sinc3 est équivalent à trois filtres sinc identiques en série, etc. — créent la réponse en fréquence. (Source de l'image : Texas Instruments)

Dans la Figure 6, les pics et les zéros sont caractéristiques de la réponse du filtre sinc. Les zéros de réponse en fréquence se produisent à f (Hz) = N ·F_D, où N = 1, 2, 3, ... Aux fréquences zéro, le filtre a un gain nul.

Les filtres sinc (en série) créent une atténuation accrue, entraînant une latence accrue. Par exemple, si un calcul spécifique de filtre sinc avec une fréquence d'horloge externe de 7,3728 MHz produit un débit de données de sortie de 14 400 éch./s, le débit de données de la sortie du deuxième filtre sinc est de 7200 éch./s.

Le filtre RIF passe-bas est un filtre basé sur le coefficient. Le filtre a une atténuation simultanée de 50 Hz et 60 Hz et des harmoniques à des débits de données de 2,5 éch./s à 20 éch./s. Le temps de latence de conversion des débits de données du filtre RIF est équivalent à un seul cycle. Le filtre RIF reçoit des données pré-filtrées du filtre sinc et décime les données pour obtenir des débits de données de sortie de 10 éch./s (Figure 7).

Figure 7 : Dans l'ADS1262/63, le filtre RIF atténue les signaux de 50 Hz et 60 Hz pour réduire les interférences de fréquence de ligne, et il fournit une série de zéros de réponse placés à proximité de ces fréquences. Les zéros se répètent aux harmoniques 50 Hz et 60 Hz. (Source de l'image : Texas Instruments)

Le filtre RIF atténue les signaux de 50 Hz et 60 Hz pour réduire les interférences de fréquence de ligne et il fournit une série de zéros de réponse placés à proximité de ces fréquences. Les zéros de réponse se répètent aux harmoniques 50 Hz et 60 Hz.

CAN ΔƩ précis à faible bruit

Un excellent exemple de CAN ΔƩ à faible bruit est le convertisseur 24 bits à entrée différentielle ADS1235 de Texas Instruments mentionné précédemment.

L'ADS1235 est un CAN ΔƩ de 7200 éch./s de précision, avec trois entrées différentielles ou cinq entrées asymétriques et un amplificateur à gain programmable (PGA) intégré avec des gains de 1, 64 et 128. Ce dispositif comprend également des fonctionnalités de diagnostic telles que les moniteurs de référence et de dépassement de gamme PGA. Le CAN fournit des données de conversion à dérive nulle haute précision, pour les équipements de haute précision y compris les balances, les extensomètres et les capteurs de pression résistifs (Figure 8).

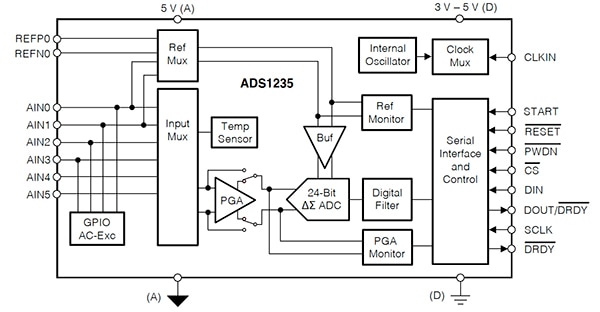Figure 8 : Schéma fonctionnel du CAN ΔƩ 24 bits ADS1235 avec entrée analogique à 6 canaux et multiplexeur d'entrée GPIO. (Source de l'image : Texas Instruments)

Pour l'ADS1235, les facteurs importants qui affectent les performances de bruit sont le débit de données, le gain PGA et le mode de découpage. Un débit de données plus lent introduit la fréquence de bruit du filtre numérique, ce qui réduit le bruit. De plus, grâce à un moyennage des données à deux points, effectué en mode découpage, le bruit diminue de √2 par rapport au fonctionnement normal.

Avec une basse fréquence, un débit de données de 2,5 éch./s et un gain PGA de 1 volt/volt, le bruit du convertisseur sur la sortie numérique sinc3 dans un système 5 V est de 0,15 mV_RMS (0,3 mV crête-à-crête (_PP)) avec une résolution effective de 24 bits, ainsi qu'une résolution sans bruit de 24 bits. Le SNR théorique, ainsi que le SNR réel de ce dispositif, sont de 146 dB. En fait, dans ces conditions, le modulateur du quatrième ordre stable et les filtres sinc1 à sinc4 produisent 24 bits de résolution effective, ainsi qu'une résolution sans bruit de 24 bits.

L'ADS1235 réalise des conversions 24 bits quasi parfaites pour un débit de données de 2,5 éch./s. Le CAN ΔƩ de génération suivante dans cette gamme est l'ADS1262/63 de Texas Instruments. La principale différence entre ces dispositifs est que l'ADS1262/63 améliore les circuits à faible bruit et offre un registre de données de sortie étendu de 32 bits.

L'ADS1262/63 est doté d'un PGA CMOS à faible bruit amélioré avec des gains de 1, 2, 4, 8, 16 et 32. Le circuit d'entrée analogique flexible inclut deux sources de courant d'excitation de capteur adaptées pour les mesures RTD directes (Figure 9).

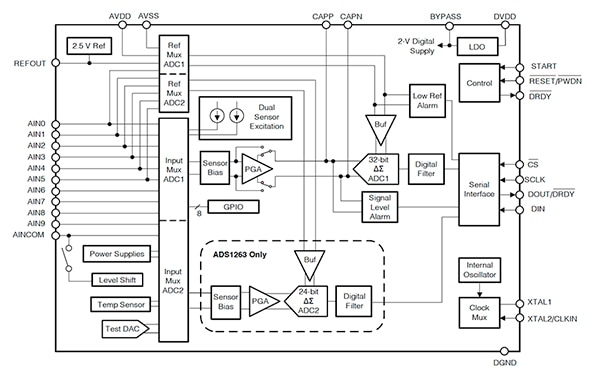Figure 9 : Schéma fonctionnel des CAN ΔƩ 32 bits ADS1262 et ADS1263 avec multiplexeur d'entrée analogique à 10 canaux. L'ADS1263 est doté d'un deuxième CAN ΔƩ 24 bits intégré. (Source de l'image : Texas Instruments)

Comme pour l'ADS1235, le gain PGA, le débit de données, le mode de filtre numérique et le mode découpage sont les principaux facteurs qui affectent les performances de bruit avec l'ADS1262/63. Avec une résolution de 32 bits, l'ADS1262/63 démontre véritablement sa capacité à atteindre une profondeur de faible bruit.

Un modulateur du quatrième ordre stable et les filtres sinc1 à sinc4 permettent initialement d'obtenir une résolution effective de 32 bits, ainsi qu'une résolution sans bruit de 24 bits. En configurant une basse fréquence, un débit de données de 2,5 éch./s et un gain PGA de 1 volt/volt (dérivé), le bruit du convertisseur de la sortie numérique sinc3 dans un système 5 V est de 0,08 mV_RMS (0,307 mV_PP). Ce dispositif dépasse la résolution effective avec 26,9 bits, et la résolution sans bruit de 25 bits. Pour ce système 32 bits, le SNR théorique est de 387 dB, le SNR réel étant de 164 dB.

Les différences entre le bruit des convertisseurs 24 bits et 32 bits sont évidentes, la capacité de faible bruit du CAN ΔƩ 32 bits dépassant celle du CAN ΔƩ 24 bits (Tableau 2).

*Note : SNR = 6,02 N + 1,76, où N est le nombre de bits

Tableau 2 : Comparaison du bruit efficace, du bruit crête-à-crête et du rapport signal/bruit du CAN avec une tension d'entrée pleine échelle de 5 V. (Source des données : DigiKey Electronics)

Conclusion

Le CAN ΔƩ continue de repousser les limites de faible bruit avec des capacités sans cesse accrues. Cet article montre comment ce CAN presque numérique à faible bruit s'intègre directement dans les applications de température, de pression et de cellules de charge. Une discussion pratique sur les CAN ΔƩ 24 bits et 32 bits de précision décrit la voie pour atteindre leurs caractéristiques ultraprécises.