Principes de base analogiques - 2e partie : CAN delta-sigma (ΔƩ) et comment exploiter leurs capacités numériques

Note de l'éditeur : Les convertisseurs analogique-numérique (CAN) connectent le monde analogique au monde numérique et sont donc un élément fondamental de tout système électronique qui se connecte au monde réel. Ils sont également un facteur déterminant quant aux performances d'un système. Cette série explore les principes fondamentaux des CAN, leurs différents types et leur application. La 1ère partie de cette série sur les principes de base analogiques est consacrée aux CAN SAR. Ici, la 2e partie traite des convertisseurs delta-sigma (ΔƩ). La 3e partie explore les CAN pipelines. La 4e partie montre comment les CAN delta-sigma peuvent générer des résultats de bruit ultrafaible. La 5e partie explore les problèmes de commande d'entrée complexes pour les CAN SAR.

Comme le montre le convertisseur analogique-numérique (CAN) à registre d'approximations successives (SAR) présenté dans la première partie, le défi de haute précision d'une chaîne de signaux de capteurs analogiques, avec de multiples gains, une mise en forme des signaux et des étages de filtrage analogiques complexes, le tout alimenté par un CAN SAR, peut conduire à des défaillances analogiques. Les concepteurs peuvent également se retrouver avec une solution coûteuse et des circuits imprimés très denses.

En outre, à commencer par des signaux ultrafaibles des capteurs, la sortie de chaque étage analogique de la chaîne de signaux engendre des erreurs qui se manifestent à la sortie numérique du convertisseur par un faible rapport signal/bruit (SNR) et des erreurs de distorsion élevées. Les concepteurs de tels systèmes doivent prendre du recul et repenser le paradigme des CAN de capteurs de haute précision.

La solution aux problèmes liés à un système de capteurs de haute précision consiste à sélectionner une topologie CAN qui numérise rapidement le petit signal du capteur et met en œuvre de manière numérique les fonctions analogiques bruyantes de gain et de filtrage. C'est le rôle du CAN delta-sigma (ΔƩ).

Cet article décrit brièvement la fonction fondamentale d'un CAN ΔƩ et les mécanismes internes de conversion analogique-numérique à l'aide d'un circuit d'entrée analogique-numérique universel servant d'exemple, à savoir l'AD4110-1 d'Analog Devices. À partir de là, il analyse la chaîne de signaux environnante et fournit des spécifications cruciales pour aboutir à un système d'acquisition de données approprié.

Structure d'un CAN ΔƩ

Juste avant le début du siècle, le CAN ΔƩ a volé la vedette à l'analogique. Avec l'adoption généralisée de la technologie avancée de convertisseurs ΔƩ, les principaux signaux analogiques et processus de calcul ont commencé à apparaître dans le domaine numérique. L'examen du circuit intégré d'un CAN ΔƩ montre que plus de 80 % des composants de la puce exécutent des fonctions numériques. Le principal avantage de la prédominance des circuits numériques tient à leur robustesse et à leur faible encombrement.

Comment cela a-t-il été possible ? Tout commence par la numérisation directe des signaux analogiques à basse tension. Une fois dans le domaine numérique, les circuits numériques peuvent presque entièrement remplacer le filtrage analogique tout en assurant les fonctions de gain requises (Figure 1). Les circuits numériques se réduisent également à chaque nœud de processus de semi-conducteurs.

Figure 1 : Un CAN ΔƩ contient presque tous les circuits nécessaires pour le filtrage et le gain. Dans cet exemple, un CAN ΔƩ détecte et numérise la faible tension du capteur de température à résistance (RTD). Il utilise ensuite le filtrage et le gain interne du signal numérique pour obtenir un résultat numérique 24 bits à faible bruit. (Source de l'image : A Baker's Dozen)

Dans la Figure 1, le système CAN ΔƩ 24 bits se compose d'une entrée analogique, d'un moteur numérique central et d'une borne E/S numérique. Le convertisseur acquiert le signal RTD à basse tension et, grâce à un filtrage numérique, produit une représentation numérique complète à 24 bits de l'entrée analogique. Il n'existe pas de bloc de gain analogique, habituellement prédominant dans les circuits CAN SAR, et le seul filtre analogique réside dans la combinaison de R₁ et de C₁. Oui, il s'agit bien d'un filtre de premier ordre simple et peu coûteux !

Principe de fonctionnement d'un CAN ΔƩ

La topologie de base d'un CAN ΔƩ comporte un modulateur ΔƩ en série avec un filtre numérique. Au-delà de cette topologie de base, la plupart des CAN ΔƩ présente une variété d'autres fonctionnalités. Cependant, tous les convertisseurs ΔƩ possèdent ce noyau essentiel (Figure 2).

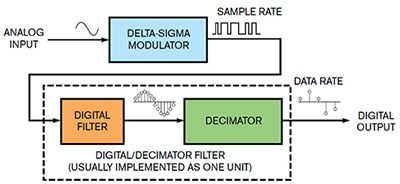Figure 2 : Pour revenir à l'essentiel, chaque CAN ΔƩ dispose d'un modulateur ΔƩ, d'un filtre numérique et d'un décimateur. (Source de l'image : EDN)

Dans la Figure 2, l'entrée peut être sinusoïdale ou CC ; nous allons ici nous concentrer sur une entrée sinusoïdale. Le modulateur ΔƩ numérise une onde sinusoïdale à cycle simple en un flux de 1 bit. La fréquence d'échantillonnage de sortie du modulateur ΔƩ est Fs. Bien que la conversion du modulateur 1 bit semble avoir une distorsion de quantification élevée, le bruit du signal est en fait « façonné » dans les hautes fréquences. Cela ouvre la voie à une conversion à faible bruit et à haute résolution à la sortie du filtre numérique.

À la sortie du modulateur, le filtre numérique accumule les résultats 1 bit du modulateur ΔƩ et effectue les calculs de filtrage. Le signal de sortie du filtre numérique reflète numériquement le signal d'entrée analogique tout en continuant avec une fréquence de sortie Fs. Le signal réside désormais exclusivement dans le domaine numérique. Un filtre passe-bas numérique, ou filtre de décimation, atténue le bruit à fréquence plus élevée et ralentit le débit de données de sortie, 1/Fd. Le filtre numérique/décimateur échantillonne et filtre le flux de code 1 bit du modulateur en un code multibit plus lent.

Alors que la plupart des convertisseurs n'ont qu'une seule fréquence d'échantillonnage, le convertisseur ΔƩ en compte deux : la fréquence d'échantillonnage d'entrée (Fs) et la fréquence des données en sortie (Fd). Le rapport de ces deux variables de fréquence définit le rapport de décimation du système (DR), selon l'Équation 1 :

Équation 1

Modulateur ΔƩ

Le modulateur ΔƩ effectue la conversion analogique-numérique proprement dite en produisant un flux de codes de 1 bit. Ce processus commence au niveau d'un amplificateur différentiel (Figure 3).

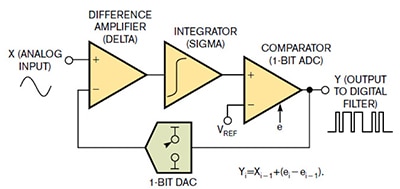Figure 3 : L'étage d'entrée du modulateur CAN ΔƩ détecte le delta entre l'entrée analogique et le CNA de rétroaction. Le deuxième étage met en œuvre une fonction d'intégrateur ou sigma sur le signal analogique. (Source de l'image : EDN)

Dans la Figure 3, l'amplificateur différentiel (delta) transmet le signal analogique à un intégrateur (sigma). À la sortie de l'intégrateur, un comparateur établit une différence à une fréquence d'échantillonnage très élevée (1/Fs) entre la sortie de l'intégrateur et une référence de tension (V_REF). En outre, le comparateur présente le flux de 1 bit au convertisseur numérique-analogique (CNA) 1 bit. Le modulateur mesure alors la différence entre le signal d'entrée analogique et la sortie analogique du CNA de rétroaction.

Le modulateur ΔƩ permet de moduler le bruit vers des fréquences plus élevées grâce à l'action de l'intégrateur et de la boucle de rétroaction du CNA. La formule de la Figure 3 (en bas à droite) montre l'équation de transfert comme suit : Y_i = X_i-1 + (e_i – e_i-1). Le modulateur numérise le signal d'entrée (X_i) en code de sortie 1 bit (Y_i) avec une distorsion de quantification (e_i). Plus précisément, la sortie du modulateur (Y_i) est égale à l'entrée (X_i-1) plus la distorsion de quantification (e_i - e_i-1). Cette formule montre la distorsion de quantification comme étant une différence entre l'erreur actuelle (e_i) moins l'erreur précédente du modulateur (e_i-1).

Filtres numériques et de décimation

Le moyennage est une forme de filtrage numérique, courante dans les CAN ΔƩ industriels à faible vitesse. Presque tous les CAN ΔƩ industriels incorporent la classe de filtres de moyennage appelés filtres sinc, qui utilisent une réponse impulsionnelle finie (RIF) à phase linéaire, ce qui correspond à un filtre passe-bas numérique (Figure 4).

Figure 4 : Les coefficients (b_x) de ce filtre numérique RIF de moyennage sont tous égaux à un. (Source de l'image : DigiKey Electronics)

Dans la Figure 4, le flux binaire de sortie du modulateur correspond à l'entrée de ce filtre numérique, et l'horloge d'échantillonnage du modulateur détermine le temps de retard. Les coefficients de la Figure 4 (b_x) pour les filtres RIF sont tous égaux à un. Grâce à cet algorithme de moyennage, le filtre numérique RIF génère une représentation numérique à faible bruit sur 24 bits de l'entrée analogique de la Figure 3, les échantillons se produisant à la fréquence d'échantillonnage du modulateur (1/Fs). Le filtre de décimation réduit ensuite le débit de données de sortie, en utilisant le rapport de décimation (DR).

Dans la littérature, le terme « décimation » se rapporte à la pratique militaire consistant à éliminer systématiquement les soldats indésirables. La décimation en électronique numérique utilise le même concept pour réduire le débit de données de sortie du signal numérique (1/Fd) par le rapport de décimation (DR). La façon numérique la plus rapide pour y parvenir consiste à éliminer systématiquement certains des échantillons de sortie du filtre numérique (Figure 5).

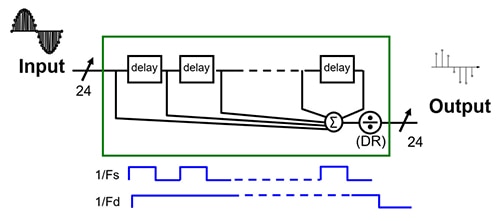Figure 5 : Le processus de décimation réduit systématiquement le nombre de sorties numériques 24 bits par un facteur du débit de données de sortie (1/Fd, en bas de l'image) divisé par la fréquence d'échantillonnage (1/Fs). (Source de l'image : DigiKey Electronics)

Le processus de décimation illustré à la Figure 5 décime le débit de données de sortie (1/Fd) par le rapport de décimation (DR), selon l'Équation 1.

Les événements traversant le filtre numérique et de décimation réduisent efficacement le bruit du CAN ΔƩ (Figure 6).

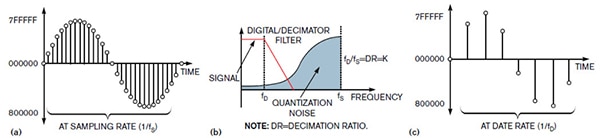Figure 6 : Cette illustration montre la sortie du filtre numérique (a) dans le domaine temporel ; la sortie en forme de bruit du modulateur superposée à la fonction passe-bas du filtre de décimation (b) ; et le signal de sortie du décimateur dans le domaine temporel (c). (Source de l'image : EDN)

La Figure 6 montre le signal numérique lorsqu'il traverse le filtre numérique/de décimation. La sortie 24 bits du filtre numérique (Figure 6(a)) fonctionne à la même fréquence que la fréquence d'échantillonnage du modulateur (1/Fs). Le modulateur a déjà façonné la distorsion de quantification en fréquences plus élevées (Figure 6(b)), de sorte que le filtre numérique/de décimation capture la partie basse fréquence du signal de sortie. La sortie du filtre de décimation (Figure 6(c)) produit une représentation numérique à basse fréquence du signal analogique d'origine.

Développement numérique

Le CAN ΔƩ réside principalement dans le domaine numérique. Il est désormais possible d'ajouter facilement des étages de gain programmables numériquement, des sources de courant, des indicateurs de signaux d'entrée en court-circuit ou en circuit ouvert et diverses interfaces de sortie série (Figure 7).

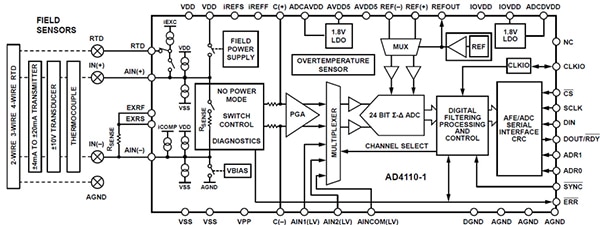Figure 7 : L'AD4110-1 d'Analog Devices offre de multiples fonctions de circuits d'entrée analogiques pour les systèmes de contrôle de processus industriels. (Source de l'image : Analog Devices)

La Figure 7 montre que le CAN ΔƩ AD4110-1 d'Analog Devices comporte de nombreuses améliorations numériques, notamment des bornes d'entrée programmables, des fonctions de diagnostic et des débits de données flexibles. Les interfaces de capteurs en entrée prêtes à l'emploi comprennent des capteurs de température à résistance et à thermocouple.

L'AD4110-1 possède le noyau de base d'un CAN ΔƩ, mais l'accent mis sur le numérique permet une série de fonctions numériques, à tel point que l'AD4110-1 est maintenant un circuit d'entrée analogique (AFE) universel.

Comme pour un CAN ΔƩ standard, l'AD4110-1 est capable de numériser des tensions extrêmement basses provenant de thermocouples, de capteurs de température à résistance et de ponts. Alors que ces fonctions nécessitent souvent des circuits d'excitation supplémentaires, l'AD4110-1 les intègre directement à son système.

Par exemple, le capteur RTD nécessite une source de courant de précision qui est ratiométrique par rapport à la référence de tension du convertisseur (Figure 8).

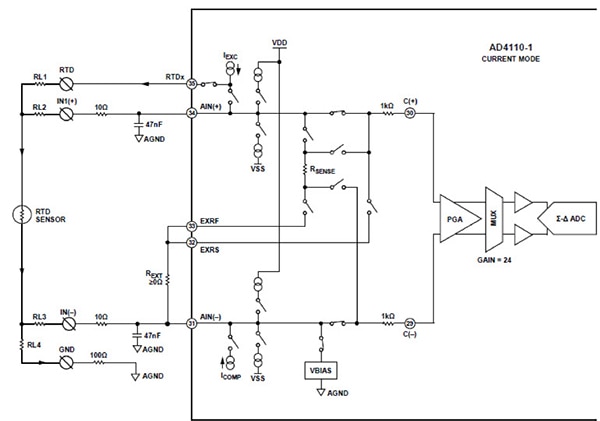Figure 8 : Connexions appropriées pour un capteur RTD à quatre fils et le CAN ΔƩ AD4110-1. Le courant d'excitation du capteur RTD est programmable à six niveaux entre 0,1 mA et 1 mA. (Source de l'image : Analog Devices)

Dans la Figure 8, l'AD4110-1 comprend un courant d'excitation qui peut être programmé à six niveaux entre 0,1 mA et 1 mA à l'aide du registre PGA_RTD_CTRL du convertisseur. Le courant d'excitation de la résistance RTD provient de la broche 35. Le convertisseur détecte la chute de tension aux bornes du RTD via les broches 34 et 31 des entrées à haute impédance. L'amplificateur à gain programmable (PGA) AD4110-1 offre 16 gains programmables de 0,2 à 24 volts/volt. Grâce à cette fonctionnalité, le concepteur est en mesure de compléter le capteur d'entrée dans la plage d'entrée de l'AD4110-1. Parmi les autres capacités auxiliaires figurent les courants d'excursion basse/haute pour détecter la présence d'un fil nu (utile avec les thermocouples), l'étalonnage du gain et les coefficients de correction.

Conclusion

Le CAN ΔƩ élimine les circuits d'entrée analogiques complexes et fournit un signal de sortie numérique à haute résolution, à faible bruit et moyenné numériquement, en utilisant un modulateur d'entrée, un filtre numérique RIF et un filtre de décimation. La plus grande partie des circuits se présentant sous forme numérique, ils peuvent être facilement dimensionnés grâce à des nœuds de processus numériques avancés, et il est possible d'ajouter davantage de fonctionnalités tout en conservant un faible encombrement et une complexité réduite des cartes.

Le CAN ΔƩ AD4110-1 d'Analog Devices tire le meilleur parti des caractéristiques de cette architecture de CAN. L'AD4110-1 possède le noyau de base d'un CAN ΔƩ, mais l'accent mis sur le numérique permet une série de fonctions numériques, à tel point que l'AD4110-1 est maintenant un circuit d'entrée analogique (AFE) universel et il est véritablement prêt pour les capteurs de température à résistance et les thermocouples.