Pourquoi et comment utiliser des filtres numériques pour la conversion analogique-numérique haute vitesse et haute résolution

Nous sommes encore dans un monde analogique, et pourtant l'électronique numérique est omniprésente, et ce pour une bonne raison. Si le numérique permet de résoudre de nombreux problèmes grâce à des approches algorithmiques, même les meilleurs algorithmes numériques présentent des lacunes lorsqu'il s'agit de traiter des entités du monde réel qui existent dans le domaine analogique. Cela est particulièrement vrai dans les applications exigeant une acquisition de données à haute vitesse et haute résolution, comme l'instrumentation, la commande moteur et les systèmes d'acquisition de données.

Le problème pour les concepteurs qui cherchent à capturer et à traiter ces signaux du monde réel est la nécessité d'entrer dans le domaine numérique le plus rapidement possible sans compromettre les informations de signal. La solution consiste en un simple algorithme de moyennage (pour réduire le bruit) avec un filtre passe-bas (LPF) analogique frontal. Grâce à ces techniques, un dispositif approprié peut fournir une conversion haute résolution et haute vitesse avec un filtrage analogique et numérique embarqué.

Cet article aborde brièvement les problèmes liés à la réalisation d'une conversion haute vitesse et haute résolution avec un convertisseur analogique-numérique (CAN) à registre d'approximations successives (SAR) utilisant un filtre passe-bas analogique et un filtre numérique à moyenne, et explique pourquoi cette combinaison de filtres constitue une bonne option pour la plupart des applications. Il présente ensuite le CAN SAR à huit canaux AD7606C-18 d'Analog Devices et montre comment tirer parti de son taux de conversion de 1 méga-échantillon/s (Méch./s), de son réseau de convertisseurs à échantillonnage simultané et de ses fonctions de filtre numérique flexibles.

Pour illustrer comment obtenir les meilleures performances globales, cet article combine l'AD7606C-18 avec la référence de tension haute précision à bruit ultrafaible ADR4525, également d'Analog Devices, pour améliorer la précision SAR requise pour les conversions 18 bits.

Filtres analogiques par rapport aux filtres numériques

Si un ingénieur analogique et un ingénieur numérique discutent de filtres, l'ingénieur numérique peut rejeter l'analogique. Ce serait une erreur. La norme de filtrage avec toute conversion analogique-numérique (A/N) est d'avoir le filtre passe-bas analogique avant le filtre numérique (Figure 1).

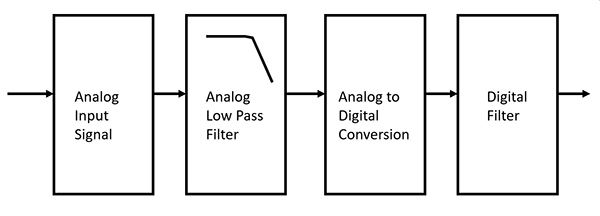Figure 1 : Schéma fonctionnel d'une chaîne de signaux analogiques-numériques avec le filtre analogique avant le filtre numérique. (Source de l'image : DigiKey Electronics)

Une fois que le filtre passe-bas analogique a atténué les fréquences plus élevées au-dessus de la bande passante d'intérêt, le CAN convertit le signal en un mot numérique. Ensuite, le filtre numérique peut agir sur le signal dans la bande passante d'intérêt.

Filtres analogiques dans les environnements d'acquisition de données

L'importance du filtre passe-bas analogique est évidente à la sortie du CAN. Tout signal traversant le CAN est associé à une amplitude et à une fréquence. À la sortie du CAN, l'amplitude du signal reste la même de manière fiable si la fréquence du signal est inférieure à la bande passante d'entrée du CAN. Bien que la conversion A/N préserve l'amplitude du signal, il n'en va pas de même pour les fréquences du signal. On peut observer un changement dans les fréquences supérieures à ½ de la fréquence d'échantillonnage du CAN, f_S, également connue sous le nom de taux d'échantillonnage de Nyquist (Figure 2).

Figure 2 : Dans le graphique (A), la représentation de transformation de Fourier rapide (FFT) d'un signal d'entrée comporte cinq composantes de fréquence. Après une conversion A/N, la représentation FFT dans le graphique (B) montre les cinq signaux se produisant en dessous de la moitié de la fréquence d'échantillonnage du CAN (f_S). (Source de l'image : DigiKey Electronics)

Dans la Figure 2, les deux tracés FFT utilisent une fréquence logarithmique sur l'axe des x et une amplitude ou une tension linéaire sur l'axe des y. Dans le graphique (A), la représentation FFT du signal analogique montre le signal d'entrée d'un CAN avec des signaux multiples ou du bruit au-dessus de la moitié de la fréquence d'échantillonnage du CAN, ou f_S/2.

En comparant ces deux graphiques, il est utile de suivre les cinq signaux FFT. Après une conversion CAN, les amplitudes du signal original restent les mêmes, mais les fréquences supérieures à la moitié de la fréquence d'échantillonnage dans (A) sont « inversées » en dessous de f_S/2 dans (B). Ce phénomène est connu sous le nom de repliement du signal. Pour acquérir le signal avec précision, la fréquence d'échantillonnage f_S du CAN doit être supérieure à deux fois f_MAX, où f_MAX est égal à la largeur de bande utilisable du signal, conformément au théorème d'échantillonnage de Shannon-Nyquist.

On peut voir comment les CAN implantent en permanence du bruit et des signaux indésirables dans le signal de sortie numérique. Ce changement rend impossible de faire la différence entre les signaux dans la bande et les signaux hors bande à la sortie du convertisseur.

On pourrait s'attendre à ce qu'il y ait un aller-retour entre ces deux représentations FFT. Cependant, une fois que cette transformation a eu lieu, il est impossible de revenir en arrière et de l'annuler. Malheureusement, les mathématiques ne permettent pas ce type de transition aller-retour.

Revenons au débat analogique/numérique : un filtre numérique est sans aucun doute capable d'appliquer un moyennage, un filtrage à réponse impulsionnelle finie (RIF) ou à réponse impulsionnelle infinie (RII), et de réduire ainsi le bruit du système. Cependant, chaque filtre numérique requiert une quantité significative de suréchantillonnage (processus d'échantillonnage d'un signal à une fréquence d'échantillonnage nettement supérieure au débit de données de sortie final), ce qui prend du temps, de l'énergie et réduit la vitesse d'échantillonnage du CAN. Le filtre numérique et la fonction de convertisseur ne permettent jamais de surmonter les phénomènes de signaux de repliement. Il est préférable de simplement réduire le bruit à plus haute fréquence dès le départ, même avec un filtre passe-bas analogique rudimentaire du premier ordre.

Moyennage des filtres numériques

Les CAN SAR améliorent leur mesure de bruit CC grâce à un filtre numérique à moyenne. Le filtre numérique à moyenne acquiert plusieurs conversions avec une échelle de temps cohérente pour augmenter le nombre de bits. Les utilisateurs de CAN utilisent des algorithmes de moyennage avec leur contrôleur, leur processeur ou un moteur de moyennage intégré qui capture plusieurs échantillons de convertisseur. Le processus de moyennage « lisse » le groupe de conversions et améliore la résolution effective par la réduction du bruit système.

La mise en œuvre du lissage des données converties implique de multiples acquisitions de signaux à une fréquence d'échantillonnage constante et le moyennage d'un nombre d'échantillons prédéterminé. Le processus de moyennage est bien connu. La somme des résultats du CAN (échantillons successifs, x) divisée par le nombre d'échantillons (N) produit une valeur moyenne (Équation 1).

Équation 1

Ce processus réduit le débit de données de sortie d'un facteur N mais augmente le temps de stabilisation du système.

L'écart-type des échantillons bruyants moyennés (σ_avg) est l'écart-type du signal original (σ_sig) divisé par la racine carrée de N (Équation 2).

Équation 2

Les échantillons successifs, y compris le bruit non corrélé, permettent de réduire davantage le bruit à une moyenne de signal constante. Chaque échantillon consécutif moyenné entraîne une amélioration du rapport signal/bruit (SNR) si le signal est continu et si la composante de bruit est aléatoire.

L'amélioration du rapport signal/bruit est proportionnelle à la racine carrée du nombre d'échantillons moyennés. Une moyenne de quatre échantillons de signaux CC (4¹) augmente la résolution effective du convertisseur de 1 avec une augmentation de 6 décibels (dB) du rapport signal/bruit. Une moyenne de 16 échantillons ou 4² augmente la résolution effective de 2 et le rapport signal/bruit de 12 dB. Avec cette logique, une taille de groupe de 4^N augmentera de N le nombre de bits effectifs d'une conversion, ce qui ramène le bruit du système à zéro et la valeur SNR à l'infini.

Variance d'Allan

Une valeur SNR égale à l'infini est bien sûr absurde. Dans le monde réel, l'acquisition du nombre requis d'échantillons prend du temps, pendant lequel le système peut changer en termes de degrés de dérive.

La variance d'Allan, ou variance à deux échantillons, mesure la stabilité de fréquence dans les horloges, les oscillateurs, les CAN et les amplificateurs en montrant la variation du bruit lorsque le nombre d'échantillons utilisés dans le moyennage d'un signal augmente. L'outil d'analyse statistique de la variance d'Allan détermine le nombre maximum d'échantillons requis optimal pour un système donné, estimant ainsi la stabilité en mettant en évidence la dérive de fréquence ou les effets de la température.

Par exemple, les données d'un système provenant d'un CAN au fil du temps peuvent présenter des décalages comme illustré à la Figure 3.

Figure 3 : Les 30 000 points de données de sortie CAN capturés pendant neuf minutes montrent une légère dérive des données sur cette période, entraînant une dégradation du calcul de la variance d'Allan. (Source de l'image : Electronic Design)

L'algorithme de variance prend plusieurs lots de moyennes de plus en plus longues et évalue le bruit résultant de chaque lot (Figure 4).

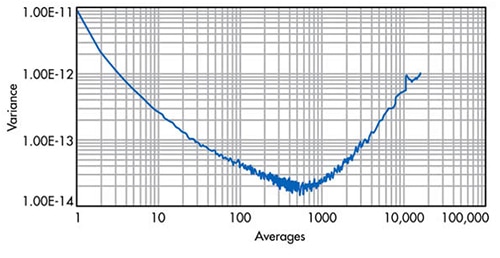Figure 4 : Calcul de la variance d'Allan appliquée aux points de données de la Figure 3. A la moyenne de 500 points, ce système CAN particulier acquiert 4,48 bits soit une augmentation du rapport signal/bruit de 27 dB. (Source de l'image : Electronic Design)

La Figure 4 montre que la variance minimum des points de données de ce système particulier se produit à environ 500 moyennes de sortie CAN — le nombre optimal de moyennes d'échantillons pour la réduction du bruit. A la moyenne de 500 points, ce système CAN acquiert 4,48 bits soit une augmentation de 27 dB du rapport signal/bruit. Avant et après le 500e point moyen, les résultats se dégradent dans la Figure 4, car la dérive des données devient un facteur plus important. Les variables qui ont un impact sur les calculs de la variance d'Allan peuvent être le temps, la stabilité du signal, la dérive, les variations de l'alimentation et le vieillissement du produit. Si un filtre à moyenne numérique est utilisé, il est prudent d'évaluer le système global avec l'outil de variance d'Allan.

Une solution concrète

Les convertisseurs SAR peuvent offrir des fonctions d'amplificateur à gain programmable (PGA) et de filtre numérique pour améliorer la résolution effective et la tension du bit le moins significatif (LSB). Par exemple, l'AD7606C-18 d'Analog Devices est un système d'acquisition de données (DAS) A/N 18 bits, à échantillonnage simultané de 1 Méch./s et avec huit canaux, chacun contenant une protection de blocage d'entrée analogique, un amplificateur à gain programmable, un filtre passe-bas et un CAN SAR 18 bits.

Le dispositif est également doté de tampons d'entrée analogiques avec une impédance d'entrée de 1 méga-ohm (MΩ) et des configurations de tension d'entrée bipolaire différentielle, bipolaire asymétrique et unipolaire asymétrique programmables. L'AD7606C-18 permet la connexion de huit canaux de signaux ou capteurs d'entrée indépendants différents.

Le filtre numérique de l'AD7606C-18 dispose d'un mode de suréchantillonnage qui fait la moyenne des échantillons répétitifs de 1 à 256 (4⁴). Selon l'outil de variance d'Allan, cette fonction de suréchantillonnage améliore les performances de bruit à la sortie numérique du convertisseur. La référence de tension de précision de 2,5 volts (V) à faible bruit ADR4525 complète le système d'acquisition de données AD7606C-18 avec un coefficient de température maximum de 1 partie par million par degré Celsius (ppm/°C) et un bruit de sortie typique de 1 microvolt (mV) crête-à-crête (Figure 5).

Figure 5 : CAN SAR AD7606C-18 avec référence de tension de précision 2,5 V ADR4525. Les inductances avec filtres passe-bas de premier ordre sur les canaux d'entrée V1 à V8 échantillonnent simultanément les huit canaux. (Source de l'image : Analog Devices)

Comme illustré à la Figure 5, ce type de réseau SAR à haute impédance d'entrée peut interfacer directement avec les capteurs, sans les amplificateurs de commande externes typiques. Un étage de gain de capteur externe peut également s'avérer inutile. Parallèlement, le convertisseur SAR est doté d'un étage PGA et LPF interne qui assure le traitement des signaux, suivi d'un filtre numérique à moyenne pour réduire davantage le bruit en offrant des résolutions effectives plus élevées. Un tel système d'acquisition des données peut offrir une résolution effective de 17,1 bits avec une vitesse de conversion de 3,9 kilo-échantillons par seconde (Kéch./s). À l'autre extrémité du spectre de vitesse de conversion, ce dispositif offre une résolution effective de 15 bits avec une vitesse de conversion de 1 Méch./s.

La vitesse de conversion la plus rapide de l'AD7606C-18 est de 1 Méch./s avec un suréchantillonnage égal à 1. Si le suréchantillonnage des canaux du convertisseur est de 2, ou si les échantillons d'un canal sont moyennés deux fois, la vitesse de conversion est la moitié de la vitesse de conversion maximum soit 500 Kéch./s. Pour un suréchantillonnage égal à 4, ou 4¹ comme nombre d'échantillons moyennés, la vitesse de conversion de ce canal est de 250 Kéch./s, et ainsi de suite. Pour chacun des huit canaux, le système avec une valeur de suréchantillonnage de 256 fournit une plage asymétrique de ±10 V, une résolution effective de 17,1 bits (rapport signal/bruit de 105 dB), avec une vitesse de conversion de 3,9 Kéch./s (Tableau 1).

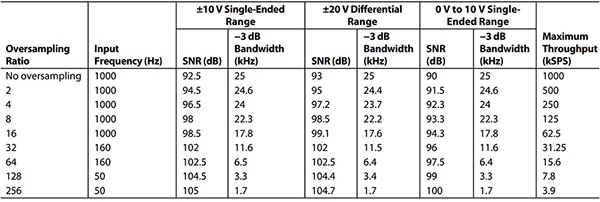Tableau 1 : Mode à faible bande passante et performances de suréchantillonnage de l'AD7606C-18. (Source du tableau : Analog Devices)

La formule de conversion SNR-résolution effective (nombre de bits effectif, ou ENOB) est présentée dans l'Équation 3.

Équation 3

À l'autre extrémité du spectre de vitesse de conversion, avec un facteur de suréchantillonnage de 1, ce dispositif offre une résolution effective de 15 bits (rapport signal/bruit de 92,5 dB) avec une vitesse de conversion de 1 Méch./s (Tableau 1).

L'AD7606C-18 offre d'autres améliorations. Comme il y a huit CAN SAR distincts sur la puce, les huit canaux ont une fonction d'échantillonnage simultané. Grâce à cette fonction, il est possible d'implémenter un filtre numérique pour atteindre une haute résolution ou une haute vitesse simultanément sur tous les canaux. De plus, tous les canaux ont une capacité d'étalonnage et de diagnostic.

Par exemple, l'étalonnage de phase système de l'AD7606C-18 détecte le décalage du filtre d'entrée discret. Cette précieuse fonctionnalité permet d'identifier tout décalage sur les composants discrets ou dans le capteur utilisé pouvant provoquer un déphasage entre les canaux échantillonnés simultanément. Le mode logiciel du dispositif compense le déphasage par canal en retardant l'instant d'échantillonnage d'un canal individuel.

L'étalonnage du gain système détecte les décalages de la résistance du filtre d'entrée discret. Cette capacité permet de surmonter les décalages des résistances externes. Le mode logiciel compense l'erreur de gain par canal en écrivant la valeur de la résistance série utilisée dans le registre correspondant.

L'étalonnage du décalage système tient compte des décalages du signal d'entrée pendant l'activité d'étalonnage. Le logiciel peut ajuster le décalage du capteur externe de chaque canal ou tout décalage de paire de résistances externes.

Pour une application spécifique, la carte EVAL-AD7606SDZ pour l'AD7606 est dotée d'un logiciel qui aide à l'évaluation du dispositif avec la programmation et l'acquisition de formes d'ondes, d'histogrammes et FFT (Figure 6).

Figure 6 : La carte d'évaluation AD7606 (à gauche) connectée à la carte de plateforme de démonstration système (SDP) (à droite), permettant de contrôler la carte d'évaluation via le port USB d'un PC. (Source de l'image : Analog Devices)

Le logiciel de la carte d'évaluation permet à l'utilisateur de configurer la valeur de suréchantillonnage de chaque canal, la plage d'entrée, le nombre d'échantillons et la sélection du canal actif. De plus, ce logiciel permet également d'enregistrer et d'ouvrir des fichiers de données de test.

Conclusion

Malgré l'évolution vers le numérique, le monde reste analogique et les concepteurs ont besoin d'une électronique centrée sur l'analogique pour résoudre les problèmes de conversion haute vitesse et haute résolution. Comme illustré, la simple combinaison d'un filtre passe-bas analogique et d'un filtre numérique à moyenne — mis en œuvre avec le nombre approprié d'échantillons moyennés — améliore considérablement les performances d'un convertisseur SAR 1 Méch./s.