Notions de base sur les filtres passe-bas antirepliement (et pourquoi ils doivent être adaptés au CAN)
Avec la contribution de Rédacteurs nord-américains de DigiKey
2020-03-24
Sans protection, les systèmes d'acquisition de données échantillonnées de base — qu'ils soient utilisés pour l'IoT, la maison intelligente ou le contrôle industriel — rencontrent des problèmes d'inexactitude dus au repliement, qui génère de faux signaux en raison du sous-échantillonnage de l'entrée analogique. Le repliement rabat les éléments de signaux dont les fréquences sont supérieures à la fréquence de Nyquist (la moitié de la fréquence d'échantillonnage) dans le spectre de bande de base, où ils ne peuvent plus être séparés des signaux souhaités, ce qui entraîne des erreurs. En outre, le bruit au-dessus de la fréquence de Nyquist est également mélangé à la bande de base, ce qui réduit le rapport signal/bruit (SNR) des signaux de bande de base souhaités.
La solution pour éviter le repliement consiste à limiter la bande des signaux d'entrée, en limitant tous les éléments de signaux d'entrée en dessous de la moitié de la fréquence d'échantillonnage du convertisseur analogique-numérique (CAN). La limitation de la bande s'effectue à l'aide de filtres passe-bas analogiques, appelés « filtres antirepliement ». Ces filtres doivent limiter la bande sans créer de distorsion du signal, de bruit ou de variations d'amplitude dans la fréquence. Les conceptions des filtres passe-bas antirepliement doivent fournir une réduction rapide et une atténuation suffisante dans la bande d'arrêt pour réduire brusquement les amplitudes des signaux supérieures à la fréquence de Nyquist.
Cet article aborde les critères de conception des filtres passe-bas antirepliement et explique pourquoi et comment ils doivent rigoureusement correspondre aux spécifications du CAN. Il présente ensuite leur mode d'implémentation avec des filtres actifs ou des filtres à capacités commutées à l'aide de dispositifs d'échantillonnage d'Analog Devices.
Qu'est-ce que le repliement ?
Le repliement se produit lorsqu'un système acquiert des données à un taux d'échantillonnage insuffisant. Si un signal contient des fréquences supérieures à la fréquence de Nyquist, ces dernières sont mélangées à la fréquence d'échantillonnage dans l'échantillonneur du convertisseur et mises en correspondance avec des fréquences inférieures à la fréquence de Nyquist, ce qui entraîne la combinaison de signaux différents et l'impossibilité de les distinguer lors de l'échantillonnage (c'est-à-dire qu'ils deviennent des versions repliées les uns des autres) (Figure 1).
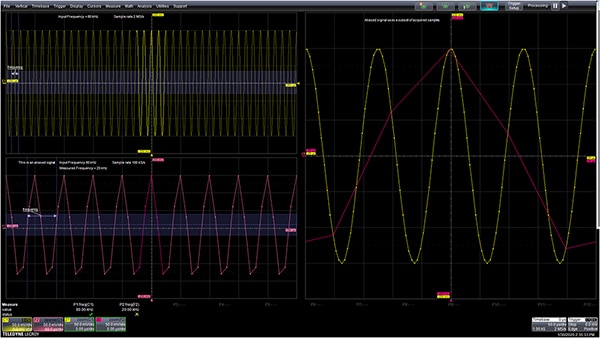 Figure 1 : Exemple de repliement. Une onde sinusoïdale de 80 kilohertz (kHz) échantillonnée à 2 Méch./s (en haut à gauche) ne présente aucun repliement. La réduction du taux d'échantillonnage à 100 Kéch./s (en bas à gauche) entraîne une interprétation du signal comme s'il avait une fréquence de 20 kHz. Le signal correctement échantillonné et le signal replié se superposent dans la vue agrandie (à droite). Les points sur le tracé représentent les échantillons. Notez que le signal replié utilise un sous-ensemble des données correctement échantillonnées. (Source de l'image : Digi-Key Electronics)
Figure 1 : Exemple de repliement. Une onde sinusoïdale de 80 kilohertz (kHz) échantillonnée à 2 Méch./s (en haut à gauche) ne présente aucun repliement. La réduction du taux d'échantillonnage à 100 Kéch./s (en bas à gauche) entraîne une interprétation du signal comme s'il avait une fréquence de 20 kHz. Le signal correctement échantillonné et le signal replié se superposent dans la vue agrandie (à droite). Les points sur le tracé représentent les échantillons. Notez que le signal replié utilise un sous-ensemble des données correctement échantillonnées. (Source de l'image : Digi-Key Electronics)
Le signal présenté en haut à gauche est une onde sinusoïdale de 80 kHz échantillonnée à 2 Méch./s. À ce taux, la fréquence de Nyquist s'élève à 1 MHz, et le signal est bien en dessous. La représentation en bas à gauche montre ce qui se passe lorsque le taux d'échantillonnage est réduit à 100 Kéch./s. La fréquence de Nyquist s'élève alors à 50 kHz et la fréquence de l'onde sinusoïdale de 80 kHz est supérieure à cette dernière, d'où son repliement.
À droite de l'image, le signal correctement échantillonné et le signal replié sont horizontalement étendus et se superposent. Les échantillons réels sont indiqués par un point. Notez que le signal replié contient un sous-ensemble d'échantillons du signal échantillonné à 2 Méch./s. L'échantillonnage est une opération de mélange, dont la sortie correspond à la somme et à la différence des signaux d'entrée et de la fréquence d'échantillonnage.
À un taux d'échantillonnage de 100 Kéch./s et à une fréquence de signal de 80 kHz, la fréquence différentielle est de 20 kHz. Les mesures de fréquence des deux cas sont illustrées sous les représentations. La mesure du paramètre P1 mesure la fréquence du signal correctement échantillonné à 80 kHz, tandis que la fréquence du signal replié est de 20 kHz.
Conception d'un filtre passe-bas antirepliement
La première étape de la conception d'un filtre antirepliement est de déterminer la largeur de bande nécessaire au système d'acquisition. Cela permet de définir la fréquence de coupure du filtre passe-bas. Les fréquences de coupure de filtre sont typiquement définies à -3 décibels (dB) ou au point à mi-puissance. Il s'agit de la fréquence à laquelle l'amplitude du signal filtré tombe à 0,707 fois l'amplitude à CC. Si la conception du système d'acquisition nécessite une réponse en fréquence plus plate, la coupure peut être définie à une valeur d'atténuation inférieure (par exemple à -1 dB). Une amplitude de fréquence de coupure supérieure renforce l'importance de la réduction de la réponse en fréquence du filtre antirepliement.
Une fois la largeur de bande du système d'acquisition déterminée, le taux d'échantillonnage peut être défini. La fréquence d'échantillonnage minimale théorique équivaut au double de la largeur de bande du système d'acquisition. Cependant, cette limite théorique ne constitue pas en pratique une bonne fréquence d'échantillonnage, car un filtre antirepliement exécutable ne peut pas atténuer les signaux supérieurs à la fréquence de coupure de manière aussi brusque qu'un filtre théorique idéal. Cela signifie que le taux d'échantillonnage doit être supérieur. En contrepartie, les exigences de mémoire augmentent avec l'accroissement de la fréquence d'échantillonnage. À l'époque des mémoires coûteuses, le taux d'échantillonnage devait être aussi proche que possible de la fréquence de Nyquist, généralement entre 2,5 fois et 4 fois la largeur de bande d'entrée. La mémoire à plus faible coût simplifie cette exigence et permet de définir un taux d'échantillonnage plus élevé pouvant atteindre cinq à dix fois la largeur de bande.
Imaginons une conception pour un capteur à ultrasons nécessitant une largeur de bande d'acquisition de 100 kHz. Le taux d'échantillonnage peut être de 500 kHz à 1 MHz.
On peut alors choisir le CAN. Pour cet exemple, il est possible de choisir un convertisseur à approximations successives 12 bits avec un taux d'échantillonnage de 1 Méch./s, comme le LTC2365ITS8#TRMPB d'Analog Devices. Sa résolution 12 bits fournit une plage dynamique théorique de 72 dB. Ce CAN présente des performances dynamiques exceptionnelles, notamment un rapport SINAD (rapport signal/bruit plus distorsion) de -72 dB et un rapport signal/bruit de -73 dB, tous les deux à une fréquence d'échantillonnage de 1 Méch./s (Figure 2).
 Figure 2 : Schéma fonctionnel et performances SINAD du CAN 12 bits à approximations successives LTC2365ITS8#TRMPB d'Analog Devices. (Source de l'image : Analog Devices)
Figure 2 : Schéma fonctionnel et performances SINAD du CAN 12 bits à approximations successives LTC2365ITS8#TRMPB d'Analog Devices. (Source de l'image : Analog Devices)
Pour un fonctionnement à un taux d'échantillonnage de 1 Méch./s, la fréquence de Nyquist est de 500 kHz. Une atténuation dans la bande d'arrêt doit être appliquée à la sortie du filtre passe-bas de 100 kHz pour abaisser les éléments de signaux supérieurs à la fréquence de Nyquist au niveau du bruit de fond du CAN, soit ici une valeur supérieure à -73 dB pour des fréquences supérieures à 500 kHz.
Sélection du type de filtre
Il existe de nombreux types ou de nombreuses configurations de filtre passe-bas. Les plus utilisés sont les filtres de Butterworth, de Chebyshev et de Bessel. Les réponses en fréquence de ces filtres varient, et ils offrent plusieurs différentiateurs clés selon l'application (Figure 3).
 Figure 3 : Comparaison des réponses en fréquence des filtres de Butterworth (gris), de Chebyshev (bleu) et de Bessel (orange). Ces types de filtre se distinguent par leur planéité de bande passante, leur temps de propagation de phase et leur pente de la région de transition. (Source de l'image : Digi-Key Electronics)
Figure 3 : Comparaison des réponses en fréquence des filtres de Butterworth (gris), de Chebyshev (bleu) et de Bessel (orange). Ces types de filtre se distinguent par leur planéité de bande passante, leur temps de propagation de phase et leur pente de la région de transition. (Source de l'image : Digi-Key Electronics)
Les réponses des trois filtres présentés ont des caractéristiques spécifiques. Par exemple, le filtre de Butterworth a une réponse en amplitude la plus plate possible. Cela signifie qu'il offre la réponse en gain la plus plate avec une fréquence dans la bande passante et avec une réduction modérée dans la région de transition.
Les filtres de Bessel offrent une temporisation uniforme pour un temps de propagation de groupe constant. Cela signifie qu'ils ont une réponse en phase linéaire par rapport à la fréquence et une excellente réponse transitoire pour une entrée d'impulsion. Cette excellente réponse en phase se fait au détriment de la planéité de la bande passante et entraîne une réduction initiale plus lente au-delà de la bande passante.
Les filtres de Chebyshev sont conçus pour fournir une réduction plus marquée dans la région de transition, mais avec plus d'ondulations dans la bande passante. Les conceptions qui utilisent ce type de filtre sont généralement basées sur une ondulation maximale donnée. Par exemple, si la limite d'amplitude de la fréquence de coupure est de -1 dB, la spécification d'ondulation est généralement définie à 1 dB maximum.
La réponse de ces filtres à une impulsion dans le domaine temporel permet de mieux comprendre quel type de filtre choisir (Figure 4).
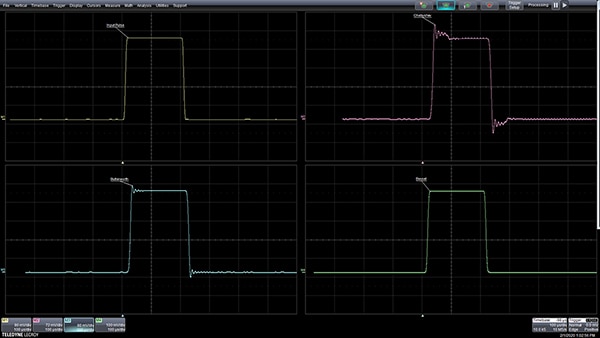 Figure 4 : La réponse des filtres à une impulsion d'entrée (en haut à gauche) montre les différences de réponse à une impulsion dans le domaine temporel des filtres de Chebyshev (en haut à droite), de Butterworth (en bas à gauche) et de Bessel (en bas à droite). (Source de l'image : Digi-Key Electronics)
Figure 4 : La réponse des filtres à une impulsion d'entrée (en haut à gauche) montre les différences de réponse à une impulsion dans le domaine temporel des filtres de Chebyshev (en haut à droite), de Butterworth (en bas à gauche) et de Bessel (en bas à droite). (Source de l'image : Digi-Key Electronics)
La réponse en phase linéaire par rapport à la fréquence du filtre de Bessel transmet l'impulsion avec une distorsion minimale, sans toutefois présenter la planéité d'amplitude du filtre de Butterworth ni la coupure brusque des filtres de Chebyshev. Le type de filtre choisi dépend de l'application :
- Le filtre de Butterworth doit être choisi si la précision de l'amplitude constitue la préoccupation majeure
- Le filtre de Chebyshev est idéal si le taux d'échantillonnage souhaité est proche de la largeur de bande de signal
- Le filtre de Bessel est la meilleure option si la fidélité d'impulsions constitue la préoccupation majeure
Ordre du filtre
L'ordre du filtre indique la complexité de la conception du filtre. Le terme fait référence au nombre d'éléments réactifs, comme les condensateurs, dans la conception. Il représente également le nombre de pôles dans la fonction de transfert du filtre.
L'ordre d'un filtre affecte la pente de réduction de la région de transition et donc la largeur de la région de transition. Un filtre de premier ordre présente une réduction de 6 dB par octave ou de 20 dB par décade. Un filtre d'ordre n présente un taux de réduction de 6 × n dB/octave ou de 20 × n dB/décade. Un filtre de 8e ordre présente donc un taux de réduction de 48 dB/octave ou de 160 dB/décade.
En se basant sur la conception de capteur à ultrasons décrite précédemment, tous les signaux supérieurs à 100 kHz doivent être atténués à au moins -73 dB à la fréquence de Nyquist de 500 kHz. Le filtre de 8e ordre atténue les signaux à environ -98 dB à 500 kHz (Figure 5). Un filtre de 6e ordre atténue un signal hors bande à 500 kHz à environ -83 dB. Ainsi, pour notre exemple, un filtre de 6e ordre serait adapté, mais un filtre de 8e ordre permettrait de fournir une amplitude encore plus basse pour les signaux hors bande. À des coûts identiques, il convient d'opter pour le filtre de 8e ordre. Ce compromis est abordé plus en détail dans la section sur les composants.
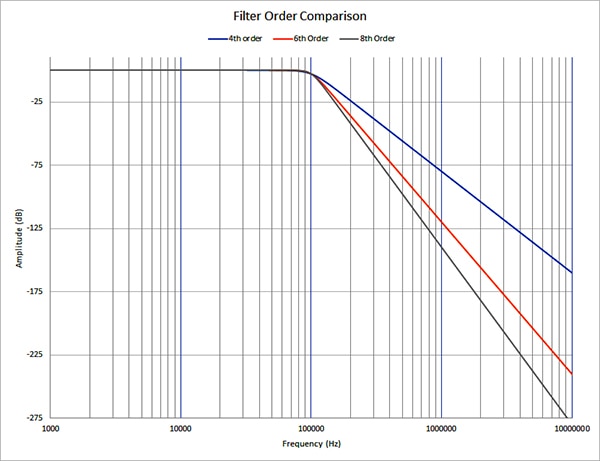 Figure 5 : Comparaison de la réduction des réponses de filtres de 4e ordre (bleu), de 6e ordre (orange) et de 8e ordre (gris). (Source de l'image : Digi-Key Electronics)
Figure 5 : Comparaison de la réduction des réponses de filtres de 4e ordre (bleu), de 6e ordre (orange) et de 8e ordre (gris). (Source de l'image : Digi-Key Electronics)
L'ordre d'un filtre peut être augmenté en associant plusieurs sections de filtre en cascade. Par exemple, deux filtres passe-bas de 2e ordre peuvent être associés en cascade pour former un filtre passe-bas de 4e ordre, et ainsi de suite. La mise en cascade de plusieurs filtres actifs entraîne en contrepartie une augmentation de la consommation énergétique, des coûts et de la dimension.
Le choix d'un filtre de 6e ordre ou de 8e ordre dépend également de la configurabilité du composant de filtre choisi. Les circuits intégrés de filtre configurés en tant que quadruples filtres de 2e ordre peuvent implémenter un filtre de 6e ordre, mais les circuits intégrés de filtre configurés en tant que doubles filtres de 4e ordre doivent implémenter un filtre de 8e ordre.
Composants de filtre
Les filtres antirepliement pour les fréquences acoustiques et à ultrasons peuvent être implémentés en utilisant des filtres actifs ou des filtres à capacités commutées. En général, les résultats sont très similaires d'un type de filtre à l'autre. Dans les applications qui utilisent des CAN très haute résolution (16 bits ou plus), le filtre actif est privilégié en raison de son potentiel de bruit inférieur. Les filtres à capacités commutées, qui nécessitent un signal d'horloge, ont un potentiel de bruit supérieur en raison de la diaphonie provenant du signal d'horloge.
La gamme LTC1563 d'Analog Devices offre des filtres actifs de 4e ordre ou à 4 pôles qui utilisent une résistance simple pour contrôler la fréquence de coupure. La gamme offre des configurations de filtre de type Butterworth et Bessel. Le LTC1563-2 est un composant de filtre de type Butterworth à 4 pôles avec une fréquence de coupure maximale de 256 kHz. Ce circuit intégré de filtre peut être associé en cascade pour obtenir une réponse passe-bas de 8e ordre (Figure 6).
 Figure 6 : Filtre de Butterworth de 8e ordre de 20 kHz implémenté à l'aide de deux dispositifs LTC1563-2 d'Analog Devices. (Source de l'image : Analog Devices)
Figure 6 : Filtre de Butterworth de 8e ordre de 20 kHz implémenté à l'aide de deux dispositifs LTC1563-2 d'Analog Devices. (Source de l'image : Analog Devices)
Si l'application nécessite une fréquence de coupure variable, le LTC1564IG#TRPBF d'Analog Devices constitue une bonne option. Ce filtre passe-bas de 8e ordre a une largeur de bande contrôlée numériquement à l'aide d'un bus de contrôle 4 bits pour varier la fréquence de coupure de 10 kHz à 150 kHz par incréments de 10 kHz. Le gain est également numériquement programmable. Le filtre présente une plage dynamique de 122 dB et est conçu pour les systèmes d'acquisition présentant une résolution de 16 à 20 bits (Figure 7).
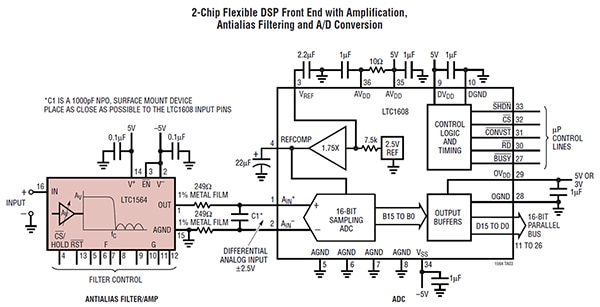 Figure 7 : Système d'acquisition de 16 bits et 500 Kéch./s utilisant seulement deux circuits intégrés. Le LTC1564IG#TRPBF fournit une largeur de bande variable jusqu'à 150 kHz et un gain jusqu'à 24 dB. (Source de l'image : Analog Devices)
Figure 7 : Système d'acquisition de 16 bits et 500 Kéch./s utilisant seulement deux circuits intégrés. Le LTC1564IG#TRPBF fournit une largeur de bande variable jusqu'à 150 kHz et un gain jusqu'à 24 dB. (Source de l'image : Analog Devices)
Des conceptions à fréquence de coupure variable peuvent également être implémentées avec des filtres à capacités commutées. Le LTC1068-25IG#PBF d'Analog Devices est un filtre passe-bas universel de 8e ordre à capacités commutées présentant une fréquence de coupure maximale de 200 kHz. Ce circuit intégré est composé de quatre éléments de filtre de 2e ordre qui peuvent être associés en cascade pour créer un filtre passe-bas de 8e ordre (Figure 8).
 Figure 8 : Filtre passe-bas de 8e ordre utilisant un filtre à capacités commutées LTC1068-25IG#PBF. La fréquence de coupure est définie à l'aide d'une horloge de commutation et est égale à la fréquence de l'horloge de commutation divisée par 32. (Source de l'image : Analog Devices)
Figure 8 : Filtre passe-bas de 8e ordre utilisant un filtre à capacités commutées LTC1068-25IG#PBF. La fréquence de coupure est définie à l'aide d'une horloge de commutation et est égale à la fréquence de l'horloge de commutation divisée par 32. (Source de l'image : Analog Devices)
Les circuits intégrés de filtres actifs universels peuvent également être utilisés pour l'antirepliement. Ils requièrent davantage de composants pour définir les caractéristiques du filtre. Le LTC1562-2 d'Analog Devices est un quadruple filtre de 2e ordre à faible bruit/distorsion qui peut être configuré comme un filtre de Butterworth, de Chebyshev, elliptique ou à réponse en temporisation à ondulations égales avec une réponse passe-bas, passe-haut ou passe-bande. Les fréquences de coupure varient de 20 à 300 kHz grâce à la programmation de la valeur de la résistance. Trois résistances programment la fréquence centrale, le gain et la valeur Q. Cette conception à quadruples filtres de 2e ordre peut être configurée pour produire des filtres de 2e, de 4e, de 6e ou de 8e ordre.
Conclusion
Les filtres passe-bas antirepliement sont nécessaires aux systèmes d'acquisition de données pour garantir la reconstruction précise des signaux échantillonnés d'intérêt. Les caractéristiques de filtre requises sont déterminées par la largeur de bande, la résolution d'amplitude et le taux d'échantillonnage du CAN auquel le filtre est couplé. Comme indiqué ici, il existe de nombreuses options de conception relatives à l'implémentation de filtres passe-bas, notamment des dispositifs actifs, à contrôle numérique et à capacités commutées.

Avertissement : les opinions, convictions et points de vue exprimés par les divers auteurs et/ou participants au forum sur ce site Web ne reflètent pas nécessairement ceux de DigiKey ni les politiques officielles de la société.







